我们应当从前文《从变差谈Cp、Cpk和Pp、Ppk》和《不谈SPC的Cpk都是耍流氓》中可以得知几个用来评价过程能力的指数之间的关系与实施评估的前提条件。但现实工作往往变幻莫测,有着各种各样的“特殊情况”;其中最典型的就是当Cp、Cpk遭遇单边公差,这时又该如何处理?
下文将根据几个常见的问题及具体案例,以及实际评价过程中可能会碰到的问题一一展开,希望能给大家带来一些启发和思考。限于个人水平有限,有理解错误或不到位的地方,烦请指正。谢谢!
问题一:单边公差真的是“单边”吗?
在实际工作当中,我们经常可以看到有规格为: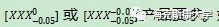 咋一看,这是典型的单边公差;对于这种情况,第一感毫无疑问是:嗯,上偏差,CPU。在根据是否大于小于1.33、1.67或其他要求来评价该过程能力是否满足要求。但现实情况真的如此吗?在回答该问题之前,请让我们来看一下单边公差的应用场景。
咋一看,这是典型的单边公差;对于这种情况,第一感毫无疑问是:嗯,上偏差,CPU。在根据是否大于小于1.33、1.67或其他要求来评价该过程能力是否满足要求。但现实情况真的如此吗?在回答该问题之前,请让我们来看一下单边公差的应用场景。

其中场景1、2、3除非采取特殊的作业方式,否则实际产品很有可能会击破单边规格要求线。也即是场景1大米的实际包装净量可能大于25.00 kg;场景2加工轴的实际长度和场景3孔/轴直径会小于25.00 mm;这类单边公差从本质上来说是“伪单边”而不是真正“单边”,它的单边是人为要求的约束界限,如前面场景1、2、3,实际会出现突破界限的情况。这种情况从专业术语来讲只能称为“单向公差”;如果把“0”改成“0.01”或其他的数值,可以称之为“非对称公差”。但如果是场景4,从自然规律来说,它就不存在平面度小于甚至等于“0”的情形;这种叫做真实的“自然界限”,多见于形位公差要求。所以,我们在评价单边公差的时候,一定要根据实际的情景,判断其是否真正的“单边”。
问题二:如何评价单边公差的过程能力?


2.1、不计算Cp;因为单边公差没有办法定义公差带宽,所以对于单边公差没有意义。2.2、Cpk取决于是上偏差还是下偏差,上偏差用CPU,下偏差用CPL。关于单标公差的Cpk大于,等于,小于Cp;这里稍微加以解释下:准确的说“2.1、不计算Cp;因为单边公差没有办法定义公差带宽,所以对于单边公差没有意义。”;如果要强行评价,只能用它的自然界限 及 公差 来定义“公差带宽”。很简单从公式可以理解。比如说:场景4平面度 Max 0.05mm。Cp = 公差带宽 / 6倍标准差 = 0.05/ 6倍标准差;Cpk = CPU =(0.05- 加工平均值)/3倍标准差;当加工的平均值大于 0.025时:Cp 大于 Cpk。当加工的平均值等于 0.025时:Cp 等于 Cpk。当加工的平均值小于 0.025时:Cp 小于 Cpk。2.3、另外还补充道:可以用物理极限(问题一提到的“自然界限”或人为要求的“约束界限”)作为替代值来计算,但和双边公差的情况下那种关系不一样。问题三:单边公差和双边公差评价方式的关系为什么不一样?
当回归到问题的本质,评价Cp、Cpk的目的是什么?其目的是为了评价该过程生产出来的产品超出规格的概率,以及该过程能力能否满足“需求”。所以在回答该问题之前得先了解一下正态分布的概率,双边超出+/-3倍的标准差时的概率为:0.135%+0.135%。这也就意味着当中心值无偏移的情况下Cpk=Cp=1时,产品良率只有1-(0.135%+0.135%)=99.73%。同样当单边公差Cpk=1时,产品的良率应当是1-0.135%=99.865%。基于此点,准确的来讲:单边公差Cpk用CPU或CPL的3倍标准差来评价和双边公差的评价应当是有那么一点点不一致的;因为和双边双尾同等Cpk的情况下,概率不完全一样(单尾和双尾的不一致,假设检验中有特意区分强调该点)。还有一种情况就是:具有真实“自然界限”的形位公差极有可能不是“正态分布”。用正态分布的概率来计算“非正态”分布的概率,毫无疑问也是不一致的。
问题四:按照AIAG要求的评价方式计算出来的Cpk真的“准确”吗?
“准确”意味着能给实际工作带来价值。作为甲方来说,毫无疑问是非常有价值的;至于原因看看《SPC手册》组委会成员就非常清楚了;通用、福特、戴姆勒克莱斯勒等确信无疑统统都是甲方。但对乙方来说就不一定。让我们回到场景来讨论问题:
作为甲方来说,希望场景一净重越大越好(望大);希望场景2、3、4稳定在目标准(望目),稳定在25.00不变,场景4平面度最好是一直为0。但现实情况大家都知道,变差是不可回避的;所以,不可能稳定在目标值不变。下文就通过Minitab来模拟场景二、三的数据来看看。4.1、计算>随机数据>正态分布;输入下面参数生成数据。将C1列命名为“左偏”。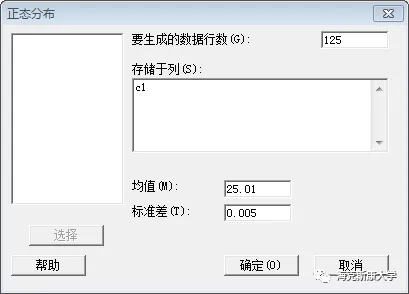
4.2、统计>质量工具>能力分析>正态(N);输入下面参数分别评价其过程能力。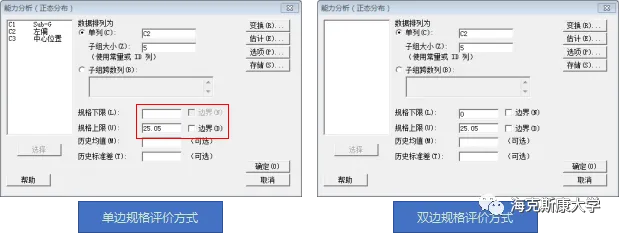
注意:该处如果是单边选择“规格下限”不输入,或者输入“0”勾选“边界”。此两种方式对结果无影响,唯一区别就是:直方图上面一个有“下限”,一个没有 “下限”。
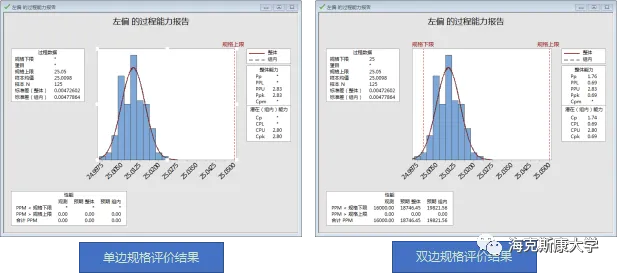
单边规格Cpk= CPU =2.80;但如果是双边规格则为:CPU=2.80 >> Cpk =0.69。为什么会出现这种情况呢?让我们接着往下看PPM < 规格下限。单边规格默认为零!!!但实际生产加工会出现约19000ppm的超出下限情况。也即意味着1.9%的不良!!!这是因为已勾选“边界”就默认如形位公差一样再显示实际物理世界不会出现小于边界的现象。也就是说,乙方必须想办法把这一部分不良筛选过滤掉。而且,从公式很明显可以看出,当实际加工的平均值远离单边规格,单边规格计算出来的Cpk越好,但对于“伪单边公差”则意味着不合格越多。所以,这种“伪单边公差”遭遇到“真单边公差”的过程能力评价方式,对乙方来说是极度的不友好的!!!总结
最后总结下“单边公差”的过程能力如何评价,详见下图。
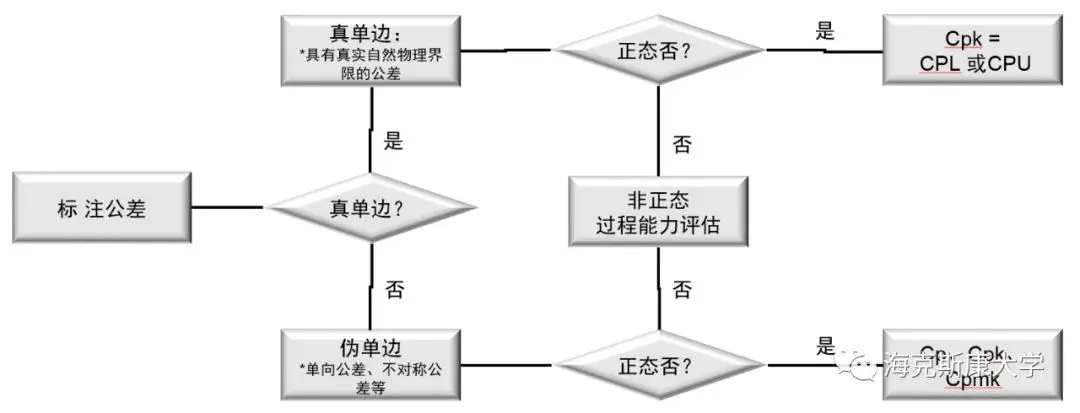
当然请别忘记过程能力评价的目的与前文提到的Cpk评价前提条件。如上文所说,其中最麻烦的是“伪单边”公差正态下的过程能力评估。至于如何解决,这里给不了明确的答案。还需要从实际过程结合具体需求着手,甲方乙方一起坐下来协调谈论出一个具体可行的接收评价标准。这时,Cp、Cpk、Cpm或许都可以是备选答案。当然,上面所说的问题对于形位公差那样的实际“自然界限”来说,统统不是问题。当伴随而来的是另外的问题,形位公差的分布极有可能不是“正态分布”。这时候非正态过程能力评估可以用得上。或许后面有空可以再来聊聊Cpm的评价和“非正态分布”的过程能力评价。名字取好了,就叫做:《从田口质量损失函数到Cpm评价》和《非正态分布如何评价其过程能力?》。







